مرتب سازی

توضیحات

مسئله‌ی مرتب سازی (Sort)، مسئله‌ای به ظاهر ساده و بسیار کربردی است. در این مسئله یک مجموعه از اعضای مشخصی که قابل مقایسه باشند، داده می‌شوند و می‌خواهیم آن‌ها را به ترتیب از کوچک به بزرگ مرتب کنیم. راه های زیادی برای این مسئله وجود دارد که در این بخش به بررسی چند مورد از معروف ترین روش های مرتب سازی خواهیم پرداخت. البته خوشبختانه ++C تابع خوبی برای سورت کردن یک مجموعه دارد که حتی می‌توان به آن یک تابع برای مشخص کردن نحوه‌ی مقایسه اعضا هم داد! با این حال درک الگوریتم‌های معروف مرتب سازی هم خالی از لطف نبوده و ممکن است برای حل بعضی مسائل مورد استفاده قرار گیرند.

عموما در این مسئله ترتیب اعضای مساوی اهمیتی ندارد و در واقع این اعضا کاملا یکسان در نظرگرفته می‌شوند. با این حال گاهی اوقات اعضا کاملا یکسان نیستند، و صرفا ممکن است در نحوه‌ی مقایسه‌ی تعریف شده، مساوی تعریف شوند. مرتب سازی پایدار (Stable sort) به نحوه‌ای از مرتب سازی گفته می‌شود که اعضای مساوی را به ترتیب ورودی میچیند. در تمام روش‌های زیر، به غیر از Counting Sort و باکت سورت، می‌توان به هر عضو از آرایه یک بخش اندیس هم به صورت پیر اضافه کرد و با سورت کردن آرایه جدید، استیبل سورت آرایه اصلی را خواهیم داشت. (البته باکت سورت به کمک ردیکس سورت می‌تواند آرایه پیر ها را هم در شرایط خاصی سورت کند) اما روش های آسان تری هم وجود دارند که در هر بخش به بررسی آن‌ها خواهیم پرداخت.

کد و الگوریتم‌های زیر به توضیح چگونگی سورت کردن یک آرایه از int پرداخته‌اند. اما به سادگی می‌توان دید روش‌های زیر به غیر از Counting Sort، باکت سورت و ردیکس سورت به ازای هر آرایه از جنس متغییرهایی که قابل مقایسه باشند، درست و امکان پذیر هستند. برای ۳ روش دیگر هم در هر بخش بررسی خواهیم کرد به ازای چه نوع از آرایه‌هایی قابل استفاده هستند.

بابل سورت

مرتب سازی حبابی یا بابل سورت، الگوریتم ساده‌ای برای مرتب‌سازی است. این الگوریتم دارای پیچیدگی زمانی \(O(n^2)\) و مموری \(O(n)\) است.

الگوریتم

فرض کنید میخواهیم آرایه \(A\) را با اندیس های \(0\) تا \(n-1\) مرتب کنیم. الگوریتم مرتب سازی حبابی \(n\) مرحله دارد. در هر مرحله جفت عضوهای متوالی دنباله به ترتیب بررسی می‌شوند و در صورت نیاز جابه‌جا می‌شوند. روند اجرای یک مرحله از الگوریتم بدین صورت است:

1. متغییر \(i\) را برابر با ۰ قرار دهید.

2. اگر \(a_i > a_{i+1}\) مکان دو عدد \(a_i\) و \(a_{i+1}\) را عوض کنید.

3. \(i\) را یکی زیاد کنید.

4. اگر \(i\) برابر \(n-1\) بود الگوریتم را پایان برسانید و در در غیر این صورت به مرحله 2 بروید.

اثبات درستی الگوریتم

یک مرحله از الگوریتم را در نظر بگیرید. فرض کنید \(x\) عضو آخر، مرتب شده باشند. (تمام \(x\) عدد ماکسیمم آرایه در \(x\) جایگاه آخر به صورت مرتب شده قرار داشته باشند) ولی عضو \(n - x - 1\) ام مقدار درستی نداشته باشد و مقداری قبل از آن و بیشتر از آن وجود داشته باشد. درواقع \(x\) را طول بزرگترین سافیکس درست در نظر بگیرید. بین باقی اعضای آرایه بزرگترین عضو را در نظر بگیرید. اگر این عضو \(b\) باشد، هنگامی که \(i\) به \(b\) می‌رسد به راحتی می‌توان دید که با جابه‌جایی‌های متوالی \(b\) در جایگاه \(n-x-1\) قرار می‌گیرد. پس در اجرای هرمرحله از الگوریتم مرتب سازی حبابی بزرگترین عضو آرایه که در جای درستش قرار ندارد، به مکان درست منتقل می‌شود. می‌توان نتیجه گرفت \(n\) بار اجرای این مراحل برای مرتب کردن آرایه کافی است.

کد

for(int j = 1; j <= n; j++)
    for(int i = 0; i < n-1; i++)
        if(a[i] > a[i+1])
            swap(a[i], a[i+1]);

استیبل بابل سورت

به راحتی می‌توان دید اگر دو عدد مجاور تنها در صورتی جابه‌جا شوند که عدد اول اکیدا بیشتر باشد، این مرتب‌سازی استیبل خواهد بود.

اینزرشن سورت

اینزرشن سورت (Insertion sort) الگوریتمی برای مرتب سازیست که در تایم \(O(n ^ 2)\) و مموری \(O(n)\) اجرا می‌شود.

الگوریتم

می‌خواهیم آرایه \(A\) به طول \(n\) را سورت کنیم. در طی \(n\) مرحله \(A\) را سورت می‌کنیم به طوری که بعد از مرحله \(i\)ام، \(i\) عضو اول دنباله مرتب شده باشند. قبل از مرحله \(i + 1\)ام عدد خانه \(i + 1\)ام از پریفکسی از اعداد کوچکتر مساوی است و برای اینکه بعد این مرحله \(i + 1\) عدد اول مرتب شده باشند باید این عدد دقیقا بعد از این پریفیکس قرار بگیرد، که برای اینکار پوینتر \(pt\) را روی خانه \(i\)ام می‌گذاریم و تا وقتی که از آرایه خارج نشدیم این عملیات را تکرار می‌کنیم:

1. اگر \(a_{pt} ≤ a_{pt + 1}\) این مرحله را تمام کن.

2. مقدار \(a_{pt}\) و \(a_{pt + 1}\) را با هم جا‌به‌جا کن.

3. از \(pt\) یکی کم کن.

اثبات درستی الگوریتم

روی \(i\) استقرا می زنیم. می‌خواهیم ثابت کنیم اگر پس از مرحله \(i\)ام، \(i\) عضو اول دنباله مرتب شده باشند، آنگاه پس از \(i + 1\)امین مرحله \(i + 1\) خانه اول آرایه مرتب شده‌اند.

اگر فرض کنیم \(a_{i + 1}\) برابر \(x\) باشد، می‌خواهیم عدد \(x\) را به \(i\) عدد اول آرایه که مرتب شده هستند اضافه کنیم. در اولین عملیات \(a_{pt + 1}\) همان \(x\) است که می‌خواهد به آرایه اضافه شود و هر بار که یک عملیات به طور کامل اجرا می‌شود این شرط درست باقی می‌ماند، که یعنی هر بار عملیات جایگاه \(x\) را نسبت به \(i\) عدد اول آرایه یکی عقب می‌آورد. \(x\) از سافیکسی از \(i\) عدد اول کوچکتر است، اگر اندازه این سافیکس \(t\) باشد، آنگاه دقیقا \(t\) عملیات کامل انجام می‌شوند.

حداکثر \(t\) عملیات انجام می‌شود چون پس از \(t\)امین مرحله یا \(pt\) از آرایه خارج شده است یا به آخرین عضو پریفیکسی رسیدیم که از \(x\) کوچکتر یا مساوی هستند و عملیات متوقف می‌شود.

حداقل \(t\) عملیات انجام می‌شود چون همه اعداد سافیکس از \(x\) بزرگترند پس در حین \(t\) عملیات اول هیچوقت شرط قسمت اول عملیات‌ها درست نیست.

پس \(x\) بین سافیکس اعدادی که از آنها کوچکتر است و پریفیکس اعدادی که از آنها بزرگتر یا مساوی است قرار می‌گیرد، که یعنی \(i + 1\) عدد اول آرایه مرتب شده‌اند.

الگوریتم اینزرشن سورت

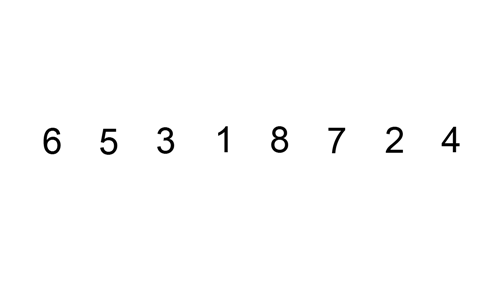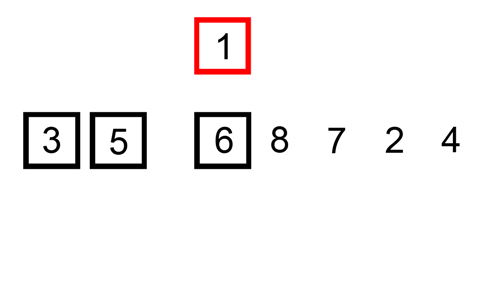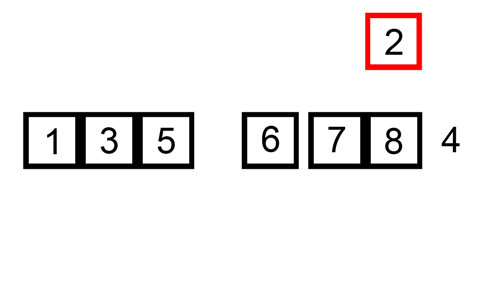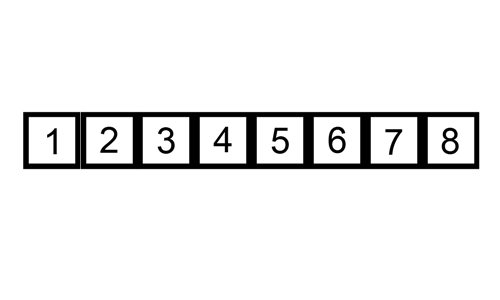
پیچیدگی زمانی

این الگوریتم \(n\) مرحله دارد و در هر مرحله حداکثر \(n\) عملیات انجام می‌دهیم، پس تایم الگوریتم از \(O(n ^ 2)\) است.

	زمان الگوریتم
بدترین حالت	\(O(n ^ 2)\)
میانگین حالات	\(O(n ^ 2)\)
بهترین حالت	\(O(n)\)

کد

int a[maxn];

for(int i = 0 ; i < n ; i++){
    int pt = i;
    while(pt > -1){ // (1)!
        if(a[pt] <= a[pt + 1]) break; // (2)!
        swap(a[pt] , a[pt + 1]);
        pt--;
    }
}

1. تا وقتی که از آرایه خارج نشدی، این عملیات را تکرار کن.

2. اگر \(a_{pt} ≤ a_{pt + 1}\) آنگاه \(x\) بین سافیکسی که از آنها کوچکتر است و پریفیکسی که از آنها بزرگتر یا مساوی است قرار گرفته است.

استیبل اینزرشن سورت

می‌توان دید اگر جابه‌جایی تنها در صورتی انجام شود که عدد اول اکیدا بیشتر باشد، این مرتب‌سازی استیبل خواهد بود.

Counting Sort

Counting Sort (سورت شمارشی) الگوریتمی برای مرتب‌سازی اعداد صحیح است که اگر اختلاف بزرگترین عضو آرایه و کوچکترین عضو آرایه برابر \(m\) باشد، در زمان \(O(n + m)\) و مموری \(O(n + m)\) اجرا می‌شود.

الگوریتم برای اعداد نامنفی

می‌خواهیم آرایه \(A\) به طول \(n\) که اعداد آن از \(m\) کوچکتر هستند را مرتب کنیم. آرایه \(cnt\) به طول \(m\) را می‌خواهیم بسازیم که در خانه \(i\)ام آن تعداد اعضای آرایه \(A\) که برابر \(i\) هستند را داشته باشیم، برای اینکار ابتدا تمام اعضای \(cnt\) را برابر صفر قرار می‌دهیم، سپس به ازای هر \(0 ≤ i ≤ n - 1\) به \(cnt_{a_{i}}\) یکی اضافه می‌کنیم. حال پوینتر \(pt\) را اول آرایه قرار می‌دهیم و به ازای \(i\) از \(0\) تا \(m - 1\)، \(cnt_{i}\) عضو بعدی آرایه را برابر \(i\) قرار می‌دهیم، برای اینکار \(cnt_{i}\) بار این عملیات‌ها را تکرار می‌کنیم:

1. \(a_{pt}\) را برابر \(i\) قرار بده.

2. به \(pt\) یکی اضافه کن

اثبات درستی الگوریتم

در آرایه پایانی تعداد دفعاتی که هر عدد ظاهر شده است برابر همان تعدادی است که در آرایه اولیه آمده، پس آرایه پایانی جایگشتی از آرایه اولیه است. همچنین آرایه پایانی سورت شده است چون قبل هر عدد تمام اعداد کوچکتر از آن در مراحل قبل به آرایه پایانی اضافه شده اند، پس آرایه پایانی همان آرایه اولیه سورت شده است.

الگوریتم Counting Sort

تعمیم برای اعداد صحیح

هر عدد را با اختلافش نسبت به کوچکترین عدد جایگزین می کنیم، حال اگر در آرایه اولیه اختلاف بزرگترین عضو آرایه با کوچکترین عضو آرایه برابر \(m\) بود، اکنون آرایه ای با اعداد نامنفی داریم که همه اعضای آن کوچکتر مساوی \(m\) هستند، که می توانیم با الگوریتم بالا این آرایه را مرتب کنیم، سپس به همه اعضای آرایه پایانی کوچکترین عضو آرایه اولیه را اضافه می کنیم و به آرایه اولیه مرتب شده می رسیم.

پیچیدگی زمانی

در این الگوریتم چند بار آرایه \(A\) را پیمایش کردیم و یک بار آرایه \(cnt\) را که در هر مرحله از این پیمایش مقداری \(pt\) را زیاد کردیم، اما \(pt\) در کل به اندازه مجموع اعضای آرایه \(cnt\) که برابر همان \(n\) است افزایش یافته است، پس الگوریتم در تایم \(O(n + m)\) اجرا می‌شود.

کد

int a[maxn] , cnt[maxm];
int mn = inf;

fill(cnt , cnt + maxm , 0);
for(int i = 0 ; i < n ; i++){
    mn = min(mn , a[i]);
}
for(int i = 0 ; i < n ; i++){ // (1)!
    cnt[a[i] - mn]++;
}
int pt = 0;
for(int i = 0 ; i < m ; i++){
    while(cnt[i]--){ // (2)!
        a[pt++] = i + mn;
    }
}

1. آرایه \(cnt\) را برای آرایه اختلاف اعضای \(A\) با کوچکترین عضو \(A\) می‌سازیم.

2. اختلاف \(cnt_{i}\) عضو بعد در آرایه سورت شده با کوچکترین عضو آرایه \(A\) برابر \(i\) است.

استیبل سورت شمارشی

این روش مرتب سازی در حالت کلی فقط برای اعداد (به طور خاص int) کاربرد دارد، ولی می‌توان دید باکت سورت حالت کلی تر و استیبل از counting sort است.

مرج سورت

مرج سورت (Merge Sort) یا مرتب سازی ادغامی، یک روش برای سورت کردن است که به نسبت روش‌های قبلی زمان اجرای بهتری دارد و از اردر \(O(n log_n)\) تایم و \(O(n)\) مموری قابل پیاده‌سازی است. این سورت به صورت بازگشتی هست و از تریک Divide & Conquer استفاده می‌کند.

الگوریتم

می‌خواهیم تابع void merge_sort(int *A, int l, int r) را پیاده سازی کنیم که بازه‌ی \([l, r)\) از آرایه \(A\) را سورت کند. \((2 \leq r - l)\) ابتدا آرایه را به دوبخش به طول های \(\lfloor \frac{r - l}{2} \rfloor\) و \(\lceil \frac{r - l}{2} \rceil\) تقسیم می‌کنیم و به صورت بازگشتی سورت می‌کنیم. سپس دو بخش سورت شده را ادغام می‌کنیم. (دو بخش \([l, \lfloor \frac{r - l}{2} \rfloor)\) و \([\lfloor \frac{r - l}{2} \rfloor, r)\)) می‌خواهیم آرایه‌ی ادغام شده را در آرایه‌ی \(r - l\) عضوی \(B\) بریزیم.

برای این‌ کار، دو پوینتر در نظر می‌گیریم که در ابتدا یکی روی عضو اول بخش اول و دیگری روی عضو اول بخش دوم قرار دارد. تا زمانی که هر دو پوینتر درون بخش ها هستند، از بین دو عضوی که پوینتر ها در حال اشاره کردن به آن‌ها هستند،‌ عضو کوچک تر را در انتهای آرایه \(B\) قرار می‌دهیم (اگر هر دو عضو برابر بودند، به دلخواه یکی را می‌گذاریم) و آن پوینتر را جلو می‌بریم. اگر یکی از پوینتر ها از بخش خودش خارج شد (به عبارتی اگر تمام اعضای آن بخش را در آرایه‌ی \(B\) قرار داده بودیم) در آن صورت به ترتیب اعضای بخش دیگر را از جایگاه فعلی پوینترش تا آخر در آرایه‌ی \(B\) قرار می‌دهیم. در آخر به ترتیب مقادیر \(B\) را در \(A_l \dots A_{r - 1}\) قرار می‌دهیم و آرایه‌ی \(B\) را پاک می‌کنیم.

مرج شدن دو آرایه

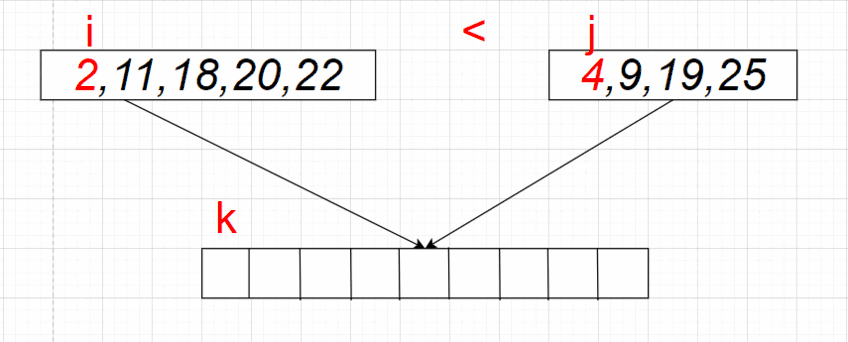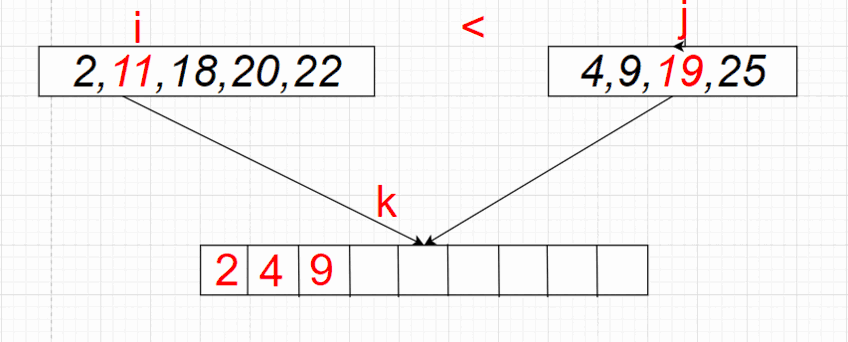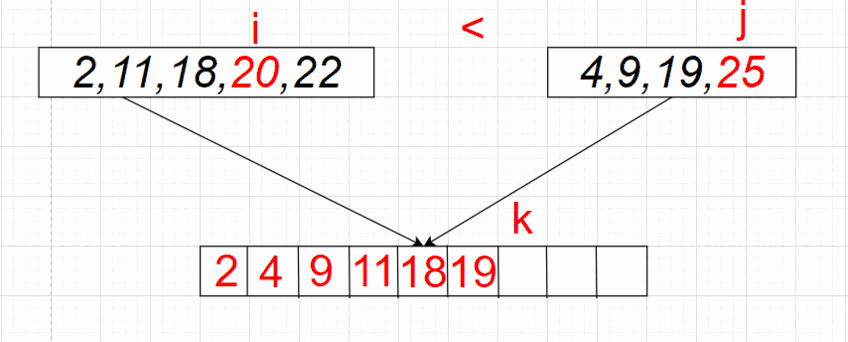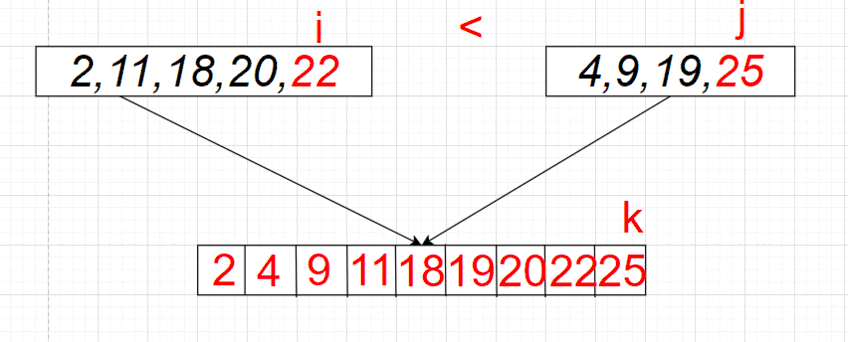
اثبات درستی الگوریتم

استقرای قوی می‌زنیم روی مقدار \(r - l\) و به کمک آن ثابت می‌کنیم الگوریتم درست است.

پایه: \(r - l = 1\) ،‌ اگر طول بازه‌ای که می‌خواهیم سورت کنیم برابر با ۱ باشد، بازه سورت شده است و نیازی به تغییر ندارد.

فرض کنید به ازای تمام مقادیر کمتر از \(r - l\) الگوریتم درست باشد،‌ برای این مقدار ثابت می‌کنیم.

طبق فرض استقرا دو بخشی که به صورت بازگشتی سورت می‌شوند به درستی سورت خواهند شد. در بخش مرج شدن، به کمک برهان خلف ثابت می‌کنیم الگوریتم درست است. فرض کنید در انتها دو اندیس ‌\(i\) و \(j\) وجود داشته باشند به طوری‌که \(i < j\) و \(B_i > B_j\). قطعا این دو عضو از یک بخش نبودند،‌زیرا هر بخش بین خودش سورت شده بود. بدون از دست دادن کلیت مسئله فرض می‌کنیم عضو \(i\) از بخش اول بوده‌است. زمانی که ما این عضو را در آرایه‌ی \(B\) گذاشتیم، پوینتر بخش دوم قطعا از بخشش خارج نشده بود و صرفا به عضوی بیشتر مساوی عضو نشان داده شده در بخش اول، اشاره داشت. (فرض کنید این مقدار از بخش دوم \(w\) باشد) همچنین قطعا پوینتر بخش دوم از عضوی که در \(B_j\) قرار داده شده‌است، نگذشته بود. و چون بخش دوم بین خودش سورت شده است:

\[B_i \leq w, \ w \leq B_j \Longrightarrow B_i \leq B_j\]

که با فرض ما در تناقض است و در نتیجه الگوریتم درست کار می‌کند.

پیچیدگی زمانی

اگر \(T(n)\)، زمان مورد نیاز برای حل مسئله در آرایه به طول \(n\) باشد،‌ داریم:

\[T(1) = O(1)\]

\[T(n) = 2 \times T(\frac{n}{2}) + O(n)\]

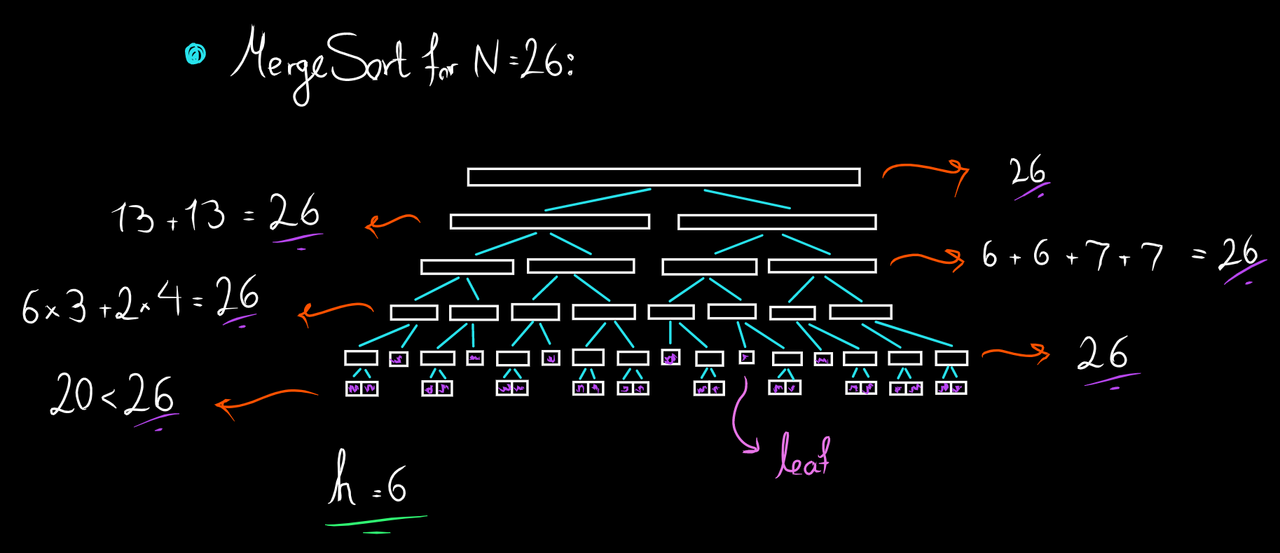
اگر تابع بازگشتی را به شکل یک درخت ببینیم، که ریشه‌ی درخت نماینده تابع مرج سورت برای \([0, n)\) باشد و بچه‌ی راس \([l, r)\)، دو تابعی بشود که توسط این راس صدا شده است، می‌توان دید مجموع طول بازه‌های راس‌های یک طبقه، کمتر مساوی \(n\) است. این درخت از \(O(log_n)\) طبقه دارد. (زیرا در هر مرحله اگر طول بازه \(len\) باشد، در بدترین حالت، به \(\lceil \frac{len}{2} \rceil\) تبدیل می‌شود. و فقط تا زمانی که به ۱ برسد ادامه دارد، پس می‌شود \(log_n + O(1)\)) هر طبقه از \(O(n)\) هزینه می‌دهد. پس در کل الگوریتم ما از \(O(n log_n)\) اجرا می‌شود. حتی می‌توان ثابت کرد الگوریتم مرج سورت از \(\Theta(n log_n)\) هم هست.

درخت توابع مرج سورت

کد

int B[maxn];

void merge_sort(int *A, int l, int r){
    if(r - l == 1) // (1)!
        return;
    int mid = (l + r) >> 1;
    merge_sort(A, l, mid);
    merge_sort(A, mid, r);
    int pt1 = l, pt2 = mid, ptB = 0;
    while(pt1 < mid || pt2 < r){ // (2)!
        if(pt1 < mid && (pt2 == r || A[pt1] < A[pt2])) // (3)!
            B[ptB++] = A[pt1++];
        else
            B[ptB++] = A[pt2++];
    }
    for(int i = r - 1; i >= l; i--)
        A[i] = B[--ptB];
}

1. در صورتی که طول بازه‌ی مد نظر برای سورت کردن،‌ ۱ باشد، بدون هیچ تغییری خارج می‌شود.

2. تا زمانی که هنوز تمام \(r - l\) عضو را ندیده‌ایم ادامه می‌دهد.

3. در این قسمت، اگر یکی از بخش ها تمام شده باشند، قطعا یک عضو از بخش دیگر برداشته خواهد شد. در غیر این صورت اگر عضو بخش اول کوچک‌تر از بخش دوم باشد، عضو بخش اول قرار داده می‌شود و در غیر این صورت از بخش دوم بر‌ می‌دارد.

تابع ‍std::merge دو بازه‌ی سورت شده می‌گیرد و این دو بازه را ادغام می‌کند. می‌توانید از این تابع هم در مرج سورت استفاده کنید. نحوه‌ی دقیق کارکرد و اطلاعات بیشتر.

استیبل مرج سورت

هنگام مرج کردن، اگر دو عضو در حال بررسی برابر بودند، ابتدا عضو بخش سمت چپ را قرار دهید.

مسئله‌ی نابه‌جایی‌ها

یک آرایه \(n\) (\(n \leq 10^6\)) عضوی از اعداد داریم. تعداد نابه‌جایی‌های این آرایه را بیابید. (لینک سوال)

نابه‌جایی چیست؟

نابه‌جایی (Inversion) در آرایه \(A\)، یک پیر از اندیس‌هایی مانند \(i\) و \(j\) است به صورتی که \(i < j\) و \(A_i > A_j\) باشد.

راهنمایی

الگوریتم مرج کردن را در نظر بگیرید و سعی کنید تعداد نابه‌جایی‌های بین بخش اول با بخش دوم را بدست آورید.

راه حل

برای حل این مسئله از تکنیک تقسیم و حل و الگوریتم مرج سورت استفاده می‌کنیم. فرض کنید در طی الگوریتم مرج سورت به صورت بازگشتی، تعداد نابه‌جایی‌های درون بخش اول و درون بخش دوم را بدست آورده‌ایم، تعداد نابه‌جایی‌های بین بخش اول و دوم را می‌خواهیم. الگوریتم مرج را در نظر بگیرید، فرض کنید اگر عضوی از بخش اول که به آن اشاره شده‌است مساوی با عضو از بخش دوم بود، عضو بخش اول را در \(B\) قرار خواهیم داد. زمانی که یک عضو را از بخش اول در آرایه‌ی \(B\) قرار می‌دهیم، این عضو از تمام اعضایی که در \(B\) هستند و از بخش دوم بودند اکیدا بزرگ‌تر بوده و با آن‌ها نابه‌جایی می‌سازد. تعداد این اعضا برابر است با \(pt2 - mid\) که \(pt2\) پوینتر مربوط به بخش دوم است و \(mid = \lfloor \frac{r - l}{2} \rfloor\) است. (بخش دوم از \(mid\) شروع شده‌است) الگوریتم ما دقیقا مشابه تحلیل اردر مرج سورت، از \(O(n log_n)\) هزینه می‌برد که مطلوب است.

کوئیک سورت

کوئیک سورت (‌Quick sort)، یک روش مرتب سازی با پیچیدگی زمانی \(O(n^2)\) و مموری \(O(n)\) است که البته از لحاظ زمانی این سورت با تغییرات جزئی قادر به رسیدن به پیچیدگی زمانی \(O(n \log n)\) است.

الگوریتم

در این روش مرتب سازی ابتدا یک عضو از آرایه را در نظر میگیریم \((x)\) . می دانیم باقی اعضای آرایه یا از \(x\) کمتر مساوی هست و یا بیشتر اکید و همچنین می دانیم در آرایه مرتب شده نهایی تمام کسانی که بیشتر اکید هستند بعد از تمام کسانی می آیند که کمتر و یا مساوی هستند در واقع اگر مجموعه اعداد بیشتر از \(x\) را \(More(x)\) و کمتر مساوی آن را \(Less(x)\) بنامیم آرایه مرتب شده نهایی به شکل

\(Sorted(Less(x)) \; , \; x \; , \; Sorted(More(x))\)

حال کافی است \(Less(x)\) و \(More(x)\) را جدا کرده به صورت بازگشتی مرتبشان کنیم و در نهایت در آرایه نهایی به ترتیب گفته شده بچینیم.

نکته

در برخی منابع به \(x\) \(،\) \(pivot\) گفته می شود.

پیچیدگی زمانی

\(T(N)\) را تعداد عملیات های لازم برای مرتب کردن یک آرایه \(N\) عضوه در نظر بگیرید. هدف این است که اثبات کنیم اگر \(x\) را به صورت رندوم از اعضای آرایه انتخاب کنیم در بدترین حالت \({T(N)} \in {O(N^2)}\) از استقرا استقاده میکنیم و پایه استقرا را \(N \leq 1\) قرار میدهیم. برای گام استقرا میدانیم

\[T(N) = T(L) + T(M) + c \times N\]

به نحوی که \(L+M = N-1\) و \(c\) عددی ثابت باشد.

حال بدون کم شدن از کلیت فرض کنید. \(L < M\) آنگاه بدست می آید

\[{T(N)} \geq {T(M) + c \times N}\]

که اگر \(M = N-1\) باشد عضو \(O(N^2)\) است.

البته اگر \(x\) را رندوم بگیریم و رندوممان خوب باشد امید ریاضی پیچیدگی زمانی مان \(O(n \log n)\) است و اگر \(x\) را برای مثال میانه آرایه مان قرار دهیم باز هم پیچیدگی زمانی مان \(O(n \log n)\) است. برای توضیحات بیشتر به لینک های پیوست مراجعه کنید.

کد

int a[maxn],tmp[maxn];

void Quick_Sort(int *a, int l, int r){ // (1)!
    if (r - l <= 1) return;

    int ind = l + rand() % (r - l), pivot = a[ind];
    int less = 0, more = 0;

    for (int i = l; i < r; i++){

        if (i == ind) continue; // (2)!

        if (a[i] <= pivot){ // (3)!
            tmp[l + less] = a[i];
            less++;
        }
        else{ // (4)!
            more++;
            tmp[r - more] = a[i];
        }
    }

    tmp[l + less] = pivot; // (5)!

    for (int i = l; i < r; i++)
        a[i] = tmp[i];

    Quick_Sort(a, l, l+less);
    Quick_Sort(a, r-more, r);

    return;
}

1. بازه بسته باز

2. \(pivot\) را حذف می کنیم به صورت موقت

3. مقادیر کمتر مساوی از سمت چپ در آرایه موقت ظاهر میشوند

4. مقادیر بیشتر از سمت راست در آرایه موقت ظاهر میشوند

5. جایگاه \(pivot\)

استیبل کوئیک سورت

بعد از انتخاب \(pivot\)، مقدار آن را در متغییری مانند \(x\) نگه دارید. در آرایه اولین تکرار \(x\) را برابر با \(pivot\) قرار دهید. هنگام بخش کردن اعضا، ترتیب بین آن‌ها را بهم نزنید و تمام اعداد مساوی با \(x\) را در بخش اعداد بزرگتر بریزید. البته روش‌های دیگری هم برای استیبل کردن کوئیک سورت وجود دارد.

باکت سورت

یکی دیگر از انواع سرت که ممکن است زیاد با آن روبرو شویم باکت سورت است. این سرت تا حد خوبی شبیه counting sort است و به تعبیری حالت کلی تر آن است. ایده کل این روش سورت این است که به ازای هر مقدار از اعضای آرایه، یک سطل درست کنیم و هر عضو آرایه را در سبد مربوطه بریزیم، و نهایتاً از سطل با کوچکترین مقدار به بزرگترین برویم و اعضای هر سطل را در آرایه جدید بریزیم، یعنی عملاً به جای اینکه تعداد هر عضو را در کاونتینگ سرت بشماریم، یک سطل برای آن قرار دارد و اعضا را در آن می ریزیم.

الگوریتم

در ابتدا آرایه ای از vectorها به اندازه \(k\) تعریف می کنیم که \(k\) حداکثر مقدار آرایه است (این آرایه را buckets می نامیم).

سپس روی آرایه از عضو اول تا انتها پیمایش می کنیم، و هر عضو آرایه را در vector مربوطه می ریزیم.

در نهایت نیز با پیمایش روی vector های آرایه محتوای vector آرایه buckets‍ را درون آرایه جواب می ریزیم.

نکته

دقت کنید این مرتب سازی stable است، زیرا هر دو عضو برابر، به ترتیبی که در آرایه بودند وارد vector مربوطه شده و به همان ترتیب درون آرایه نهایی ریخته می شوند.

پیچیدگی زمانی

در قدم اول، آرایه ای به سایز \(k\) تعریف می کنیم که انجام این عمل از \(O(k)\) است. سپس در مراحل بعد یک پیمایش روی آرایه داریم که در هر گام عملی از \(O(1)\) انجام می دهیم، و در آخر روی تمام \(k\)تا vector فور می زنیم و روی هر کدام پیمایشی از اردر اندازه اش انجام می دهیم، لذا چون مجموع تعداد اعضای اینها \(n\) است (هر اندیس آرایه در دقیقاً یکی از وکتورها است) این هم از \(O(n+k)\) است. لذا پیچیدگی زمانی در نهایت از \(O(n+k)\) است.

کد

void bucket_sort(int arr[], int n, int k) { // (1)!
    vector<int> buckets[k + 1]; 
    for (int i = 0; i < n; i++) {
        buckets[arr[i]].pb(i);
    }

    int ans[n];

    int ind = 0; // (2)!
    for (int i = 0; i < k; i++) {
        for (auto v : buckets[i]) {
            ans[ind] = v;
            ind++;
        }
    }

    for (int i = 0; i < n; i++) {
        arr[i] = ans[i];
    }   
}

1. خود آرایه، طول آن و در نهایت \(k\)

2. شمارنده ای که نشان می دهد الان می بایست کدام عضو آرایه را پر کنیم.

این سورت تنهای برای اعداد (به طور خاص int) قابل استفاده است. اما به نحوی غیر مستقیم در سورت جنس‌های دیگری هم می‌تواند به کار آید که در بخش ردیکس سورت توضیح داده شده است.

ردیکس سورت

ردیکس سورت به تعبیری حالت کلی تر باکت سورت است، سورتی که در آن \(n\) آرایه \(l\) عضوی که اعضایشان بین \(1\) تا \(k\) است را از اردر \(O(l(n + k))\) به ترتیب لغت نامه ای مرتب می کند. این سورت به نوعی شامل \(l\) باکت سورت مجزا است.

الگوریتم

به ترتیب از عضو \(l\)ام تا اول \(x\) را پیمایش کنید و در هر گام آرایه را برحسب عضو \(x\)با باکت سورت مرتب می کنیم.

اثبات درستی الگوریتم

با استقرا ثابت می کنیم بعد از مرحله \(x\) ام اعضای آرایه بر حسب اعضای \(x\) تا \(l\) مرتب شده اند.

*پایه استقرا* (\(x=l+1\) یا همان قبل از شروع پیمایش):

آرایه بر حسب \(0\) عضو انتهایی مرتب شده است.

*گام استقرا* (نتیجه گیری برای \(i\)):

بعد از این مرتب سازی، اعضای آرایه بر حسب عضو \(i\) ام مرتب شده اند. ضمناً هیچ دو عضوی پیدا نمی شوند که شرط را نقض کنند، زیرا برای مثال اگر آرایه اندیس \(i\) از اندیس \(j\) بر حسب اعضای \(x\) تا \(l\) بزرگتر باشد‌ (\(i \le j\)) در آن صورت قطعاً در دو عضو \(x\) باید برابر باشند مگرنه در باکت سورت حال حاضر اندیس \(j\) از \(i\) عقب میفتاد، ضمناً نمی توانند بر حسب اعضای \(x+1\) تا \(l\) هم بزرگتر باشند، زیرا طبق فرض استقرا در مرحله قبلی \(j\) قبل تر از \(i\) بود و حال با stable بودن باکت سورت به قطع این شرایط حفظ می شود. لذا حکم ثابت شد.

پیچیدگی زمانی

در این مرتب سازی پیچیدگی هر سورت از \(O(n+k)\) است و چون اینکار \(l\) بار تکرار می شود، نهایتاً از \(O(l(n+k))\) می شود.

ردیکس سورت در اعداد

برای سورت کردن یک آرایه \(n\) عضوی از اعداد،‌ می‌توان آن‌ها را در مبنای \(b\) نوشت. اگر \(l\) طول بزرگترین عدد آرایه در مبنای \(b\) باشد، می‌توان با ردیکس سورت اعداد را در \(O(l (n + b))\) مرتب کرد. مثلا ممکن است بخواهید به جای سورت کردن اعداد در بازه 1 تا \(1e9\) از \(O(n log_n)\)، آن‌ها را با ردیکس سورت در \(O(n)\) با ضریب ۱۰ (برای مبنای ۱۰) و یا با جمع در مقدار ثابت \(1e5\) و ضریب ۲ (برای مبنای \(1e5\)) سورت کنید.

ردیکس سورت در آرایه‌های غیر عددی؟

اگر آرایه ای از جنسی به غیر از اعداد داشته باشیم که بتوان آن‌ها را به \(l\) بخش تقسیم کرد به‌طوری‌که سورتی به روش کتابخانه‌ای روی آن‌ها در نهایت سورت کلی آرایه را بدهد، می‌توان از ردیکس سورت استفاده کرد. البته باید بتوان مقادیر در هر بخش را بین خودشان سریع مقایسه کرد. هر مرحله یک آرایه \(rnk\) نگه می‌داریم که نشان بدهد هر المنت تا این مرحله از سورت چه مرتبه‌ای دارد. البته مقدار \(rnk\) برای المنت‌هایی که تا اینجا برابر بودند را هم برابر قرار می‌دهیم. اگر طول آرایه \(n\) باشد، می‌توان طوری اعداد \(rnk\) را قرار داد که ماکسیمم این اعداد حداکثر \(n\) بشود. مثلا با این روش می‌توان آرایه‌ای از پیر دو عدد را سورت کرد. همچنین می‌توان آرایه‌ای از استرینگ ها را هم در \(O(len \times (n + A))\) سورت کرد. (\(A\) سایز الفبا و \(len\) ماکسیمم طول استرینگ هاست) البته روش‌های دیگری هم برای استفاده از \(rnk\) و ردیکس سورت وجود دارد.

کد

void bucket_sort(vector<int> arr[], int n, int k, int x) { // (1)!
    vector<int> buckets[k + 1];

    for (int i = 0; i < n; i++) {
        buckets[arr[i][x]].pb(i);
    }


    vector<int> ans[n];

    int ind = 0;
    for (int i = 1; i <= k; i++) {
        for (int j = 0; j < sz(buckets[i]); j++) {
            swap(ans[ind], arr[buckets[i][j]]); // (2)!
            ind++;
        }
    }


    for (int i = 0; i < n; i++) {
        swap(arr[i], ans[i]);
    }
}

void radix_sort(vector<int> arr[], int n, int k, int l) {
    for (int x = l - 1; x >= 0; x--) {
        bucket_sort(arr, n, k, x);
    }
}

1. آرایه، طول آن، ماکسیمم مقدار آن و اندیسی که می خواهیم بر حسب آن مرتب کنیم.

2. معادل همان برابر قرار دادن که برای \(O(1)\) بودن به این شکل نوشته شده.

استیبل ردیکس سورت

اگر تمام مراحل (شامل مرحله‌ی اول سورت) از روشی استیبل استفاده شود می‌توان دید در نهایت هم سورت استیبل خواهد بود.

منابع بیشتر

• std::sort
• Insertion Sort
• Selection Sort
• Counting Sort
• Merge Sort
• Randomized Quick Sort
• Quick sort using median
• Radix Sort

سوال ها

سوال	سختی	تگ ها	جاج
Subsequence Permutation	800	Spoiler مرتب سازی	Codeforces
Merge Sort	800	Spoiler مرتب سازی	Spoj
Distinct Numbers	900	Spoiler مرتب سازی	CSES
Subarray Sums II	1100	Spoiler پریفیکس سام مرتب سازی	CSES
out of sorts	1400	Spoiler مرتب سازی	Usaco
Inversions	1600	Spoiler تقسیم و حل fenwick مرتب سازی	SGU
Enemy Is Weak	1900	Spoiler تقسیم و حل fenwick مرتب سازی	Codeforces
Gluttony	2000	Spoiler مرتب سازی	Codeforces
Cow Photography	2500	Spoiler مرتب سازی	Usaco

نظرات