توابع بازگشتی

توضیحات

توابع بازگشتی درواقع توابعی هستند که در طول اجرا، خودشان را دوباره صدا می‌زنند. این توابع به نحوی پیاده‌سازی می‌شوند که پایانی وجود داشته باشد و تابع تا ابد ادامه پیدا نکند. عملکرد توابع بازگشتی تاحدودی استقرا طور است. این توابع حتما قسمت‌های پایه‌ای دارند که در این حالت‌ها، تابع دوباره فراخوانده نخواهد شد. بقیه حالات هم با استفاده از تابع برای حالت‌های دیگری حل خواهند شد. برای مثال تابع زیر برای عدد نامنفی \(n\)، مقدار \(n\) را می‌دهد. اما اگر عدد منفی باشد، تا جایی که بتواند بازگشتی پیش می‌برد و از آنجایی که هیچ گاه به پایه lev == 0 نخواهد رسید، به خاطر استفاده بیش از حد از توابع بازگشتی احتمالا با رانتایم ارور یا محدودیت مموری مواجه خواهد شد. (مموری‌ها و ارور استک اور فلو) از نظر منطقی هم تابع برای اعداد منفی پایان ناپذیر خواهد شد.

int f(int lev){
    if(lev == 0) // (1)!
        return 0;
    return f(lev - 1) + 1; // (2)!
}

1. پایه‌ی تابع بازگشتی

2. فراخوانی همین تابع به صورت بازگشتی برای مقادیر کمتر

توجه کنید که لزومی ندارد یک تابع فقط یکبار خودش را صدا بزند و ممکن است چندین بار از همان تابع استفاده شده باشد!

نحوه‌ی عملکرد توابع بازگشتی را می‌توان به صورت یک درخت نمایش داد. به طوری که هر مرحله از تابع را به صورت یک رأس نمایش می‌دهیم و آن را به رئوس نماینده‌ی توابعی که صدا زده وصل می‌کنیم. ریشه درخت هم معمولا تابع اولیه هست که توسط بقیه قسمت های کد فراخوانی شده است. برای مثال در تابع بالا، درخت آن یک مسیر ساده خواهد بود که در lev == 0 پایان خواهد یافت. (البته برای اعداد منفی، مسیری بی نهایت خواهد بود)

مسئله فیبوناچی

کد زیر، عدد فیبوناچی ‌\(n\)ام را به صورت بازگشتی محاسبه می‌کند.

long long fibonacci(int n){
    if(n <= 2) // (1)!
        return 1;
    return fibonacci(n - 1) + fibonacci(n - 2); // (2)!
}

1. \(F_1 = F_2 = 1\)
2. \(F_n = F_{n - 1} + F_{n - 2}\)

درخت توابع فیبوناچی

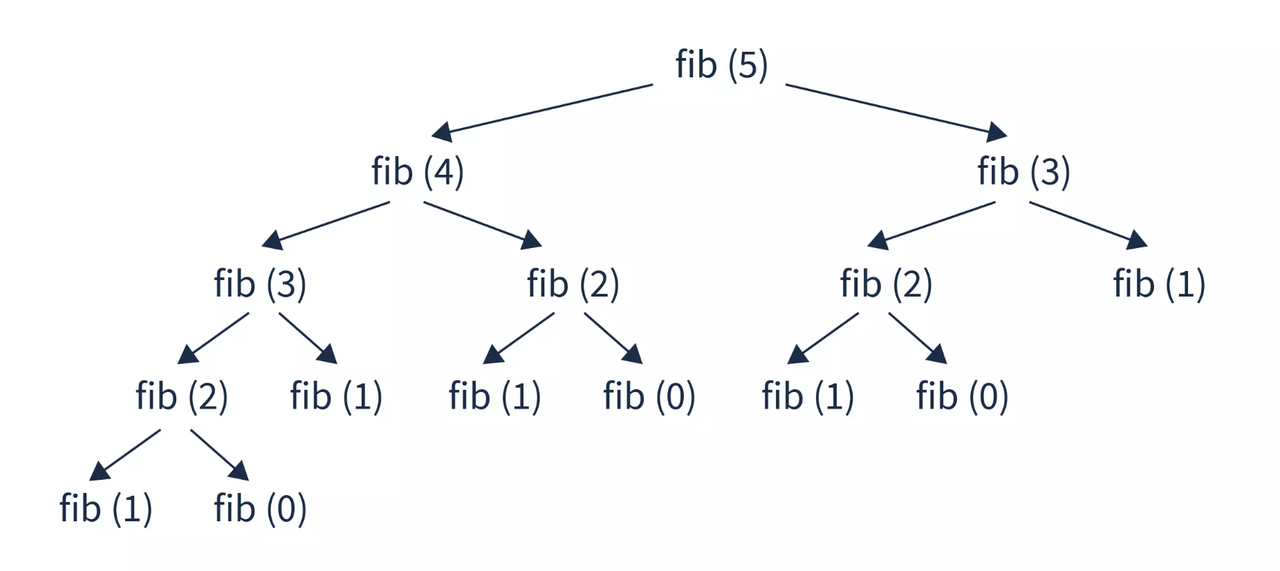
پیچیدگی زمانی

کد بالا، از \(\Theta (F_n)\) هزینه میبرد. می‌توان با بررسی درخت متوجه شد که برگ‌ها \(F_1\) و \(F_2\) هستند که برابر با ۱ هستند. تمام رئوس دیگر صرفا مجموع جواب بچه‌هایشان را محاسبه می‌کنند. پس ما به \(F_n\) تا برگ نیاز خواهیم داشت. همچنین چون هر راس غیر برگ لاقل ۲ بچه دارد، تعداد آن‌ها هم حداکثر \(F_n\) هست که در مجموع می‌شود از \(\Theta (F_n)\).

مثال‌های بیشتر

می‌توانید درخت توابع بازگشتی پیچیده تری را در قسمت مرج سورت مشاهده کنید.

بک‌ترک

الگوریتم های بک‌ترک (Backtracking Algorithms)، الگوریتم‌هایی هستند که برای پیدا کردن جواب مسئله تمام حالات مطلوب را به صورت بازگشتی ساخته و پیمایش خواهند کرد. حتی ممکن است این الگوریتم‌ها با پیمایش کل حالات در جستجوی مقدار خاصی باشند، نه صرفا تمام حالات.

مسئله جایگشت‌ها

کد زیر تمام جایگشت‌های \(n\)تایی را خروجی می‌دهد. تابع perm از جایگاه ۰ تا ind - 1 را با اعدادی که هنوز استفاده نشده‌اند می‌پوشاند. بدین ترتیب اگر در ابتدا تابع perm(n) فراخوانده شود، خروجی تمام جایگشت‌های ‌\(n\) تایی خواهد بود.

int n, a[maxn];
bool mark[maxn];

void perm(int ind){
    if(ind == 0){ // (1)!
        for(int i = 0; i < n; i++)
            cout << a[i] << ' ';
        cout << endl;
        return;
    }
    for(int i = 1; i <= n; i++) if(!mark[i]){ // (2)!
        mark[i] = true; // (3)!
        a[ind - 1] = i;
        perm(ind - 1); // (4)!
        mark[i] = false;
    }
    return;
}

1. تمام اعداد چیده شده‌اند و یک جایگشت ساخته شده است.

2. اگر \(i\) استفاده نشده بود، می‌خواهیم مقدار \(ind - 1\) ام از جایگشت ما برابر با \(i\) باشد.

3. مقدار mark[i] را true می‌کنیم تا مشخص شود استفاده شده است.

4. ادامه‌ی جایگشت را به صورت بازگشتی می‌سازیم.

پیچیدگی زمانی

اگر درخت این توابع را در نظر بگیرید، می‌توان دید تعداد برگ‌ها \(n!\) است. و هر کدام از رئوس دیگر نیز لاقل دو بچه دارند، پس تعداد رئوس درخت از \(\Theta (n!)\) است. در هر تابع هم مستقل از توابع دیگری که صدا می‌شوند، از \(\Theta (n)\) هزینه می‌دهیم. پس در کل این کد از \(\Theta (n \times n!)\) زمان می‌برد.

البته می‌توان برای ساخت تمام جایگشت‌های به طول \(n\) از next_permutation هم استفاده کرد.

ممویز کردن

ممویز کردن (Memoization)، روشی برای بهینه‌سازی زمان اجرای بعضی الگوریتم هاست. به طور خاص در الگوریتم‌های بازگشتی، می‌توان خیلی از توابع که چندین بار در حال محاسبه هستند را حذف کرد. به طور مثال در مسئله‌ی فیبوناچی، می‌توان هر بار یک مقدار از فیبوناچی محاسبه می‌شود آن را نگه داریم تا سری بعدی صدا شدن این تابع، نیازی به محاسبه‌ی دوباره نباشد. با این کار درخت توابع بازگشتی تبدیل به یک مسیر می‌شود که صرفا تعدادی یال به آن اضافه شده است. زمان اجرای کد از \(\Theta (F_n)\) به \(O(n)\) کاهش خواهد یافت! زیرا هر مقدار از 1 تا \(n\) حداکثر یکبار محاسبه می‌شود و هر تابع مستقل از توابعی که صدا می‌کند از \(O(1)\) است.

long long fib[maxn];

long long fibonacci(int n){
    if(n <= 2)
        return 1;
    if(fib[n] != 0) // (1)!
        return fib[n];
    fib[n] = fibonacci(n - 1) + fibonacci(n - 2);
    return fib[n];
}

1. اگر این مقدار از قبل محاسبه شده است، آن را برمی‌گرداند و دیگر محاسبه نمی‌کند.

هرس کردن

این روش، با حذف بعضی شاخه‌ها از درخت توابع بازگشتی مسائل بک‌ترک، زمان اجرای این توابع را بهتر می‌کند. درواقع بعضی از زیردرخت‌ها از یک درخت هیچ حالت مطلوبی را شامل نمی‌شوند و اگر بتوان سریع متوجه این موضوع شد، می‌توانیم کلا وارد آن‌ها نشویم. برای درک بیشتر، مسئله‌ی زیر را در نظر بگیرید:

مسئله پریش

به یک جایگشت از اعداد \(1\) تا \(n\)، پریش گفته می‌شود اگر هیچ عنصری در مکان خودش نباشد. به عبارتی اگر جایگشت را با \(\langle p_1, p_2, ..., p_n \rangle \,\) نشان دهیم، شرط \(p_i \neq i\) برای تمامی اعضا برقرار باشد. چند جایگشت پریش \(n\) تایی وجود دارد؟

یک روش برای حل این مسئله، ساختن تمام جایگشت‌ها و چک کردن پریش بودن یا نبودن آن‌ها در انتهاست. با این کار از \(\Theta (n \times n!)\) هزینه خواهیم داد. خیلی از این جایگشت‌ها نامطلوب هستند ولی ما تمام آن‌ها را تا آخر ساخته‌ایم. می‌توان به جای این کار، هر جایگشت را صرفا تا اولین جایی که مقدار جایگاهی از آن برابر با خودش شد، ادامه داد.

int n, a[maxn];
bool mark[maxn];

void perm(int ind){
    if(ind == 0){
        for(int i = 0; i < n; i++)
            cout << a[i] << ' ';
        cout << endl;
        return;
    }
    for(int i = 1; i <= n; i++) if(!mark[i] && ind != i){ // (1)!
        mark[i] = true;
        a[ind - 1] = i;
        perm(ind - 1);
        mark[i] = false;
    }
    return;
}

1. تنها در صورتی \(i\) را در این خانه می‌گذارد که \(i\) برابر با اندیس این خانه نباشد و استفاده هم نشده باشد.

با این کار، زمان اجرا بسیار کاهش میابد. شاید نتوانیم دقیقا مشخص کنیم چقدر بهتر می‌شود، اما به طور واضحی خیلی از جایگشت‌ها از زمان خوبی قطع شده و ادامه داده نمی‌شوند.

منابع بیشتر

• الگوریتم‌های بازگشتی
• بک‌ترک و تفاوت‌های آن با بازگشتی
• ممویز کردن

سوال ها

نیاز به عضویت در گروه شاززز!

برای حل برخی از سوالات باید ابتدا در گروه شاززز عضو شوید.

سوال	سختی	تگ ها	جاج
فاکتوریل	800	Spoiler پیاده سازی توابع بازگشتی	Quera
الگویابی	800	Spoiler توابع بازگشتی	Shaazzz
پریش	900	Spoiler توابع بازگشتی	Shaazzz
Permutations	900	Spoiler توابع بازگشتی	LeetCode
Generate Parentheses	900	Spoiler توابع بازگشتی	LeetCode
کاشی‌کاری	1000	Spoiler توابع بازگشتی	Quera
بی‌ فاصله	1000	Spoiler توابع بازگشتی	Shaazzz
جم‌زی	1000	Spoiler توابع بازگشتی	Shaazzz
اول‌دایره	1000	Spoiler توابع بازگشتی	Shaazzz
شتر	1000	Spoiler توابع بازگشتی	Shaazzz
1000-digit Fibonacci number	1000	Spoiler توابع بازگشتی پیاده سازی	Project Euler
Combinations	1000	Spoiler توابع بازگشتی combinatorics	LeetCode
Next Permutation	1200	Spoiler توابع بازگشتی	LeetCode
Easy modified sudoku	1200	Spoiler توابع بازگشتی	Spoj
Little Queens	1300	Spoiler توابع بازگشتی	SGU
The Towers of Hanoi Revisited	1500	Spoiler توابع بازگشتی	SGU
Xor	1800	Spoiler توابع بازگشتی	Codeforces

نظرات